Deriving the Shallow Water Equations

This post shows the derivation of the shallow water equations. These equations describe the flow velocity and height of the water’s free surface when the horizontal extent is much greater than the depth. For example, tidal or oceanic flows can be well modelled by these equations. They are derived directly from the Euler equation for inviscid flows.

Flow Geometry

---

We consider the depth of the water at each point, with a spatially varying bathymetry. This geometry is shown here:

We can easily convert the fluid depth (\(h\)) and the bathymetry (\(b\)) into a height above (or below) a reference height (\(\eta\)). For geophysical flows, for example, this would be the geoid. Note that \(b\) is the seafloor depth (below reference), so it has the opposite sign to \(\eta\), the height. Consequently we have \(h = \eta - b\).

Derivation

---

The shallow water equations are derived from the divergence free condition and the incompressible Euler equation, which describe mass- and momentum balance respectively, for the full 3D fluid:

$$\nabla\cdot\mathbf u = 0 \label{div_u}\tag{1}$$

$$\Dfrac{\mathbf u}{t} = -\frac{\nabla P}{\rho} + \mathbf f \label{euler}\tag{2}$$

We want to convert these into equations describing the net horizontal components of the velocity, and the fluid depth.

The net horizontal motion of the fluid is obtained by depth averaging the underlying fluid velocity. If we denote the 3D velocity components as \(\mathbf u = (u, v, w)\), then the net velocity’s x-component is given by

$$\bar u(x, y, t) = \frac{1}{h}\zint{u(x, y, z, t)} \label{uavg}\tag{3}$$

And similarly for \(\bar v\), meaning we get the 2D velocity field \(\bar{\mathbf u} = (\bar u, \bar v)\).

Conservation of Mass & the Fluid Height

---

The derivation begins by integrating the divergence free condition for the fluid, \eqref{div_u}, in the vertical direction.

$$ \zint{\Big[{\color{#e2c576} \pfrac{u}{x}} + {\color{#92d8e6} \pfrac{v}{y}} + {\color{#be98df} \pfrac{w}{z}}\Big]}= 0 $$

The z term can be handled directly by the Fundamental Theorem of Calculus. For the x and y terms, we want to pull the spatial derivatives outside the integral, but the integrals’ bounds (\(-b\) and \(\eta\)) depend on position. Therefore, in order to pull the spatial derivatives outside, we must take care to apply the Leibniz integration rule correctly. Applying this gives us the following:

$$\begin{align} 0 = &{\color{#e2c576} -u({\small z=\eta}) \pfrac{\eta}{x} - u({\small z=-b})\pfrac{b}{x} + \pfrac{}{x}\zint{u} } \\ &{\color{#92d8e6} -v({\small z=\eta}) \pfrac{\eta}{y} - v({\small z=-b})\pfrac{b}{y} + \pfrac{}{y}\zint{v} } \\ &{\color{#be98df} +w({\small z=\eta}) - w({\small z=-b}) \vphantom{\zint{}}} \end{align}$$

Reordering the terms, and using equation \eqref{uavg}

$$\begin{flalign} && 0 = &\pfrac{(h\bar u)}{x} + \pfrac{(h\bar v)}{y} & \\ && &-\Big({\color{#7bd97e} u({\small z=-b})\pfrac{b}{x} + v({\small z=-b})\pfrac{b}{y} + w({\small z=-b}) }\Big) & \text{Seabed} \\ && &-\Big({\color{#d58080} u({\small z=\eta})\pfrac{\eta}{x} + v({\small z=\eta})\pfrac{\eta}{y} - w({\small z=\eta}) }\Big) & \text{Surface} \\ \end{flalign}$$

The next step is to identify the boundary condition terms arising from the integrals.

Sea-floor Boundary Condition

The first boundary condition is simple enough; the fluid’s velocity at the seabed must be tangential to the seabed itself. If it were not, the fluid would penetrate through the sea floor or leave a vacuum. Mathematically this condition states that the fluid velocity vector is orthogonal to the seabed’s normal vector, i.e.

$${ \mathbf u({\small z = -b}) \cdot \nabla(z + b(x, y))} = 0$$

Expanding the gradient and performing the dot-product gives us exactly the seabed boundary terms above (highlighted green), so we see these terms all disappear.

Free Surface Boundary Condition

The second boundary condition is slightly subtler. The height of the free-surface at any given position can change in time. However, relative to this vertical motion, the fluid’s velocity must still be tangential to the free surface*. To see why this makes sense, imagine sitting in a reference frame where the free surface (at position \(x\)) is stationary, then we get effectively the same condition as at the seabed.

The vertical speed of the free surface is \(\pfrac{h}{t}\hat{\mathbf z}.\) Thus, using the same construction for a normal vector as above,

$$\Big(\mathbf u({\small z=\eta}) - \pfrac{h}{t}\hat{\mathbf z}\Big)\cdot\nabla(z - \eta(x, y)) = 0$$

Expanding this and rearranging yields

$$-\Big({\color{#d58080} u({\small z=\eta})\pfrac{\eta}{x} + v({\small z=\eta})\pfrac{\eta}{y} - w({\small z=\eta}) }\Big) = \pfrac{h}{t}$$

So, finally, we can plug this into the equation above for our free surface boundary condition and get

$$\boxed{ \pfrac{h}{t} + \nabla\cdot(h\bar{\mathbf u}) = 0 \label{dhdt}\tag{4} }$$

This equation describes mass conservation in the fluid with a free surface. The resulting 2-dimensional flow is no-longer divergence free, we can accommodate non-zero divergence by either “piling up” fluid at a point, or draining it away.

This is the same equation as the usual mass conservation equation for compressible fluids, with the fluid’s height now taking the place of density!

Equation \eqref{dhdt} is in conservation form. By expanding the spatial derivative we can convert it to Lagrangian form:

$$\Dfrac{h}{t} = -h\nabla \cdot \bar{\mathbf u} \label{DhDt}\tag{5} $$

The Long-wavelength Limit & Velocity Components

---

Now we turn to the momentum conservation equations, i.e. Euler’s equation. To make progress here we have to make a long-wavelength assumption.

The long-wavelength limit is that in which things vary over horizontal length-scales much greater than the fluid’s depth. This means the changes in the vertical direction also have to be slow, and the vertical acceleration is approximately zero. Therefore the \(z\) component of the Euler equation becomes

$$-\frac{1}{\rho}\pfrac{P}{z} - g = \Dfrac{w}{t} \approx 0$$

where we have used the fact that the vertical component of the body force is gravity alone. Integrating with respect to \(z\) gives

$$P = - \rho g z + C$$

We can fix the integration constant by noticing that at the surface we must have atmospheric pressure, so

$$P_0 = - \rho g \eta + C$$

thus

$$P = P_0 - \rho g (z - \eta)$$

This is the pressure profile we would get in hydrostatic equilibrium. This shows the long-wavelength limit is equivalent to assuming we are approximately at hydrostatic equilibrium. Now we can plug this into the horizontal components of Euler’s equation. Focusing on just the x-component, this gives

$$\begin{align} \Dfrac{u}{t} &= -\frac{1}{\rho}\pfrac{P}{x} + f_x \\[0.2em] &= -g \pfrac{\eta}{x} + f_x \\[0.2em] \end{align}$$

All that remains now is to depth-integrate this equation. However, here we run into a snag; the left-hand side is not linear, and so we can’t just pull the integral through the material derivative.

Thus we make our second assumption: that the horizontal components of the velocity do not vary with depth. By expanding the material derivative on the left-hand side, and identifying \(u\equiv\bar u\) and \(v\equiv\bar v\), we get

$$\Dfrac{\bar u}{t} = -g \pfrac{\eta}{x} + f_x \label{DuDt}\tag{6}$$

where now the left-hand side is a 2D material derivative, for the 2D depth averaged velocity.

Equation \eqref{DuDt} is in Lagrangian form; let’s convert it to the conservation form.

To do this it is easier to consider the total x-momentum \(h\bar u\)¹, rather than the velocity \(\bar u\). The material derivative obeys the usual product rule, therefore

$$\begin{align} \Dfrac{(h\bar u)}{t} = \pfrac{(h\bar u)}{t} + \bar{\mathbf u}\cdot \nabla (h\bar u) = h\Dfrac{\bar u}{t} + \bar u\Dfrac{h}{t} \\[0.2em] \end{align}$$

Now plug in equations \eqref{DhDt} and \eqref{DuDt} for the material derivatives on the right-hand side, and use the product-rule in reverse for the spatial gradients (highlighted in yellow)

$$\begin{align} \pfrac{(h\bar u)}{t} + {\color{#e2c576} \bar{\mathbf u}\cdot \nabla (h\bar u)} &= h\Big(-g\pfrac{\eta}{x} + f_x\Big) + {\color{#e2c576} \bar u (-h\nabla\cdot \bar{\mathbf u})} \\[0.2em] \pfrac{(h\bar u)}{t} + {\color{#e2c576} \nabla\cdot (h\bar u \bar{\mathbf u})} &= -gh\pfrac{\eta}{x} + hf_x \\[0.2em] \end{align}$$

The derivation is identical for the y component.

This completes the derivation. Henceforth, we will only ever consider the two dimensional velocity, so I’ll drop the overbar.

Shallow Water Equations in Conservation Form

---

The full shallow water equations in conservative form read

$$\begin{align} \pfrac{h}{t} + \nabla \cdot (h \mathbf u) &= 0 \\[0.2em] \pfrac{(h\mathbf u)}{t} + \nabla \cdot (h \mathbf u \otimes \mathbf u) &= -gh \nabla \eta + h \mathbf f \end{align}$$

The first equation has no source terms (zero right-hand side), which tells us that mass is exactly conserved. The water column depth can (and does) change both in space and time, but throughout the system as a whole, fluid is neither created nor destroyed.

The second equation does have source terms, telling us that momentum is not conserved. This is not surprising, the change in momentum comes exactly from the body forces experienced by the fluid. These being gravity for the vertical direction, and any other forces in the horizontal directions (e.g. Coriolis force.)

It is a simple matter to write these in terms of the displacement height \(\eta\), we just substitute in \(h= \eta + b\), yielding

$$\begin{align} \pfrac{\eta}{t} + \nabla \cdot (\eta \mathbf u) &= {\color{#92d8e6} -\nabla\cdot(b\mathbf u)} \\[0.2em] \pfrac{(\eta\mathbf u)}{t} + \nabla \cdot (\eta\mathbf u \otimes \mathbf u) &= -gh \nabla \eta + h \mathbf f \,{\color{#92d8e6} - \nabla\cdot(b \mathbf u \otimes \mathbf u)} \end{align}$$

We gain extra source terms for both equations (highlighted in blue), which represent the effect of the bathymetry on the fluid’s height.

Comments on the Derivation

---

In order not to break up the flow of the derivation with asides and notate bene, I have put these observations into this separate section.

Tong presents a very terse & understandable description of the derivation, but with the caveat that he treats only the case of uniform bathymetry. Because the seabed has a uniform depth, the bottom boundary condition becomes a condition purely on \(w,\) and the Leibnitz terms arising from moving the depth integral inside the horizontal spatial derivatives become zero.

Free Surface Boundary Condition

The free surface boundary condition seems to be presented differently between sources. For example, in Segur and Tong it is given as

$$\Dfrac{\eta}{t} = w({\small z = \eta})$$

Rather than the “no relative normal flow” condition used in Dawson & Mirabito.

This seems to make sense, but it actually relies on identifying the x and y components of the 3D velocity at the surface, with the 2D depth averaged velocity. This is something you can validly do only if you’ve already made the second assumption (uniform horizontal velocity profile).

Only the “no relative normal flow” criterion correctly applies to the 3D velocity, avoiding the need to make the uniform horizontal velocity profile at this early point in the derivation. (In Segur they have not explicitly made this assumption when using the boundary condition. However, they do make it later on, meaning it comes out in the wash.)

One doubt I had about the “no relative normal flow” constraint was; why we do not need to account for the fact the free surface is changing shape? I suppose it’s because the divergence free condition is something that must be obeyed at all instants of time and at every location separately.

Depth Integration of the Euler Equation

At the point we integrate the Euler equation we made the uniform horizontal velocity profile assumption. This lets us identify the horizontal components of the 3D velocity with the 2D depth averaged velocity, and side-step the vertical integration.

Had we not made this assumption, we would have obtained an equation very similar to equation \eqref{DuDt}, but with extra terms arising from the interaction of the non-linear advection term and the integration. Dawson & Mirabito mention this, but they do not give the form of these terms. They refer to them simply as “differential advection terms” (differential here meaning the velocity is different at different depths,) and make the second assumption by assuming these terms are zero.

Analogous to the way the distribution of microscopic velocities in the Boltzmann equation leads to diffusion of momentum (see here), I expect these terms (which are associated with the distribution of horizontal velocities) would manifest as a kind of “viscosity”.

Linearization & Gravity Waves

---

In their full glory, the shallow water equations contain many non-linear terms. We can linearize them by assuming the velocity \(\mathbf u\) and height \(\eta\) are only small perturbations away from zero. In this way, any cross terms of \(\mathbf u\) and \(\eta\) are even smaller, and we can neglect them. So, simply dropping all non-linear terms in equations \eqref{dhdt} and \eqref{DuDt} gives

$$\begin{align} \pfrac{\eta}{t} &= - \nabla \cdot(b\mathbf u) \label{detadt_linear}\tag{7} \\[0.5em] \pfrac{\mathbf u}{t} &= -g\nabla \eta + \mathbf f \label{dudt_linear}\tag{8} \end{align}$$

Note that the water column depth \(h=\eta+b\) may be large because \(b\) can be large. Moreover, remember that \(b\) is a fixed profile, so it does not count as making things non-linear.

It is simple to show that the linear Shallow water equations give rise to gravity waves, as one might expect. For this, let’s assume a constant depth \(b=B\), and no horizontal body force (\(\mathbf f = 0\)). First, take the time derivative of equation \eqref{detadt_linear} then substitute in equation \eqref{dudt_linear}:

$$\begin{flalign} && \partial_{tt}{\eta} &= -\partial_t \nabla\cdot(B\mathbf u) & \text{Differentiate} \\[0.5em] && &= -B\nabla\cdot (\, \partial_t\mathbf u) & \text{Commutativity} \\[0.5em] && &= -B\nabla\cdot (-g\nabla \eta) & \text{Substitute \eqref{dudt_linear}} \\[0.5em] && &= gB\nabla^2 \eta & \text{Distribute} \end{flalign}$$

which is the wave equation with \(c = \sqrt{gB}\). This matches the result one obtains from dimensional analysis.

The fact the wave speed depends on depth is often used as an explanation for why waves break on the beach. The argument goes like this: as a wave climbs the beach the depth, and thus \(c\), decreases. Thus the faster water from behind catches up to the slower water ahead. Eventually there is so much water piling up that it becomes unstable and overtops.

If we don’t assume constant depth and no body force, we merely gain a couple of extra terms, turning our wave equation into an inhomogeneous wave equation.

Alternative Derivation

---

Here is another derivation of the shallow water equations, which utilizes the divergence theorem. This derivation is based directly on the notion of conservation, and so it directly gives us the conservative form.

Consider a finite sized water column, of arbitrary cross-section. Denote the cross-section of the water column by \(A\), its boundary by \(\partial A\), and the unit normal to the boundary as \(\hat{\mathbf n}.\)

The derivation considers the flow of fluid & momentum through the sides, and into the water column.

Mass Conservation

---

The inflow of fluid through any side is given by

$$q = \int_{-b}^\eta \mathbf u\cdot(-\hat{\mathbf n})\,dz = -(h\bar{\mathbf u})\cdot\hat{\mathbf n}$$

\(\hat{\mathbf n}\) is the outward unit normal, hence the minus sign. We can write the net inflow as

$$Q = - \oint_{\partial A} (h\bar{\mathbf u})\cdot\hat{\mathbf n} \,dl $$

The divergence theorem tells us

$$Q = - \int_A \nabla\cdot (h\bar{\mathbf u})\,dA$$

Now coming from the other side, because our fluid is incompressible, the change in volume of fluid inside our region \(A\) must manifest as a change in the water’s depth. Therefore

$$Q = \int_A \pfrac{h}{t} \,dA$$

We did not specify anything about the size nor shape of region \(A\), therefore the integrands themselves must be equal giving

$$\pfrac{h}{t} = -\nabla\cdot (h\bar{\mathbf u})$$

which is the same as our mass conservation equation \eqref{dhdt}.

I actually find this derivation a bit more natural, but I have not seen it presented anywhere. Perhaps it contains an error I’ve not spotted? Maybe using the incompressibility to say flow results in a height change, while physically correct, is jumping the gun?

Momentum Conservation

---

For the momentum, this conservation view point is not simpler than the derivation presented above, because there identifying \(u\equiv\bar u\) avoids the depth integration. However, I will include the alternative derivation, partly for completeness, and partly because it gives a different perspective (Eulerian vs Lagrangian.)

As above, I’ll show the derivation for the x-component of velocity only. The y-component is derived in exactly the same manner.

The x-momentum flow into the water column through any side is given by

$$\begin{align} j = - \zint{u\mathbf u \cdot \hat{\mathbf n}} = -(h\bar u \bar{\mathbf u} + \Delta\bar{\mathbf u})\cdot\hat{\mathbf n} \end{align}$$

where \(\Delta\bar{\mathbf u}\) represents the “differential advection terms” discussed above. From here on we make the uniform horizontal velocity profile assumption and set \(\Delta\bar{\mathbf u} = 0.\)

We then integrate this over the whole surface of the water column to get the total momentum flux into the volume, and apply the divergence theorem

$$\begin{align} J &= - \oint_{\partial A} h\bar u\bar{\mathbf u}\cdot\hat{\mathbf n} \,dl \\[0.2em] &= - \int_{A} \nabla\cdot( h\bar u \bar{\mathbf u}) \,dA \label{J_as_div}\tag{9} \end{align}$$

Similarly to above, let’s consider the change of momentum throughout the volume. Here, however, we must be careful because we now have sources of momentum in the volume; namely the forces the fluid feels. The total rate of change of momentum at any point is the sum of the advection (momentum flow) and source (force) terms. Thus the change of x-momentum in our volume due only to advection is

$$J = \int_{A}\zint{\pfrac{u}{t} - \Big(\!-\!\frac{1}{\rho}\pfrac{P}{x} + f_x\Big)}\,dA$$

Now we make the long-wavelength / hydrostatic assumption exactly as above, then vertically integrate.

$$\begin{align} J &= \int_{A}\zint{\pfrac{u}{t} - \Big(\!-\!g\pfrac{\eta}{x} + f_x\Big)}\,dA \\[0.2em] &= \int_{A} \pfrac{(h\bar u)}{t} - \Big(\!-\! hg \pfrac{\eta}{x} + hf_x\Big)\,dA \\[0.2em] \end{align}$$

We have again used the identification \(u\equiv\bar u\) in this step.

Equating this with equation \eqref{J_as_div} and noting that \(A\) was completely arbitrary gives immediately

$$\pfrac{(h\bar u)}{t} + \nabla\cdot(h\bar u\bar{\mathbf u}) = -hg\pfrac{\eta}{x} + hf_x$$

completing the derivation.

References

---

Standard Errors of Volatility Estimates

Sample Variance

---

The sample variance is given by the formula

$$ S^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i - \bar X)^2 \label{sample_var}\tag{1}$$

where \(\bar X\) is the sample mean

$$ \bar X = \frac{1}{n} \sum_{i=1}^n X_i $$

Equation \eqref{sample_var} is an unbiased estimator for the population variance \(\sigma^2\), meaning

$$\EE{S^2} = \sigma^2$$

The variance of the sample variance is given by

$$\var{S^2} = \frac{\sigma^4}{n}\left(\kappa - 1 + \frac{2}{n-1}\right)$$

where \(\kappa\) is the population kurtosis (raw, not excess!) Note \(\kappa \geq 1\) always.

The standard error of the sample variance is

$$\varepsilon({S^2})=\frac{\std{S^2}}{\sigma^2} = \sqrt{\var{S^2}} = \sqrt{\frac{\kappa-1}{n} + \frac{2}{n^2-n}}$$

For large \(n\) this becomes

$$\varepsilon(S^2) \approx \sqrt{\frac{\kappa-1}{n}}$$

Ultimately the standard error of the sample variance scales as \(\varepsilon \sim n^{-1/2},\) similarly to the standard error of the sample mean.

Sample Standard Deviation

---

The population standard deviation - \(\sigma\) - is given by the square root of the population variance. Similarly, the sample standard deviation - \(S\) - is given by the square root of the sample variance.

We know that \(S^2\) is an unbiased estimator for \(\sigma^2,\) so Jensen’s inequality tells us that \(S\) must be a biased estimator for \(\sigma;\) specifically it is an underestimate. Jensen’s inequality states that, for any concave function \(\phi,\) we have

$$\mathbb E[\phi(X)] \leq \phi(\mathbb E[X])$$

The square-root function is concave and so

$$\mathbb E[S] = \mathbb E[\sqrt{S^2}] \,\,\leq\,\, \sqrt{\mathbb E[S^2]} = \sqrt{\sigma^2} = \sigma$$

Although \(S\) is a biased estimator for \(\sigma,\) it is consistent. That is, as \(n \rightarrow \infty\) we do get \(S \rightarrow \sigma.\)

What is the standard error on the sample standard deviation? Jensen’s inequality makes it hard to derive any fully general results. However, for large \(n\) we can derive a result.

Note that because \(\varepsilon \sim n ^{-1/2}\) as \(n\) gets large the distribution of \(S^2\) gets tighter around \(\sigma^2.\) Taylor expand \(\sqrt{S^2}\) around \(\sigma^2:\)

$$ \sqrt{S^2} = \sqrt{\sigma^2} + \frac{S^2 - \sigma^2}{2\sqrt{\sigma^2}} + O\big((S^2 - \sigma^2)^2\big) $$

Keeping only the first order term, we get

$$S = \sigma + \frac{S^2 - \sigma^2}{2\sigma} \label{S_large_n}\tag{2}$$

Now we can calculate the variance of this first order estimate of \(S:\)

$$\begin{align} \mathrm{Var}(S) &= \mathrm{Var}\Big(\sigma + \frac{S^2 - \sigma^2}{2\sigma}\Big) \\ &= \mathrm{Var}\Big(\frac{S^2}{2\sigma}\Big) \\ &= \frac{1}{4\sigma^2}\mathrm{Var}(S^2) \\ &= \sigma^2 \frac{\kappa - 1}{4n} \end{align}$$

On the last line we have used our large \(n\) approximation for \(\mathrm{Var}(S^2)\) because we already put ourselves in that regime in order to use the Taylor expansion approximation.

Taking the square-root and dividing by the population standard deviation yields

$$\varepsilon(S) = \sqrt{\frac{\kappa - 1}{4n}}\qquad\qquad n\gg 1 \label{err_S}\tag{3}$$

The argument above is a bit sloppy, I have not said under what conditions the first order approximation equation \eqref{S_large_n} is valid, nor proven when its variance is equal to the variance we seek (i.e. that of the unapproximated \(S\).) To make the argument rigorous see the “Delta Method”.

Sums of IID Random Variables

---

Let \(X_i\) be iid random variables with mean and standard deviation \(\mu_X\) and \(\sigma_X\) respectively. Define

$$Y = \sum_{i=1}^n X_i$$

We know

$$\mathbb E[Y] = n\mu_X \equiv \mu_Y \qquad\text{and}\qquad \mathrm{Var}(Y) = n\sigma_X^2 \equiv \sigma_Y^2 $$

Further, we get a similar relation for the kurtosis

$$ \kappa_Y - 3 = \frac{1}{n}(\kappa_X - 3) $$

We want to estimate the underlying standard deviation \(\sigma_X\) from observations of \(Y.\) We know \(\sigma_X = \sigma_Y / \sqrt{n},\) so we can use \(S_X = S_Y / \sqrt{n}\) as an estimate. Say we have \(m\) observations of \(Y,\) and \(m \gg 1,\) then from above we know

$$\std{S_Y} = \sigma_Y \sqrt{\frac{\kappa_Y - 1}{4m}}$$

Substituting in our known relationships we get

$$\std{S_Y} = \sqrt{n}\,\sigma_X \sqrt{\frac{(\kappa_X-3)/n + 2}{4m}}$$

we know

$$\std{S_X} = \std{\frac{S_Y}{\sqrt n}} = \frac{1}{\sqrt n}\std{S_Y}$$

so

$$\std{S_X} = \sigma_X \sqrt{\frac{(\kappa_X-3)/n + 2}{4m}} \label{S_err_nm}\tag{4}$$

The kurtosis of \(X_i\) can either reduce the standard error on our estimate (for \(\kappa_X < 3\)) or increase it (for \(\kappa_X > 3\).)

The dependence on \(n\) arises purely because of the effect of the summation on the overall kurtosis of \(Y.\) Additionally as \(n\) grows the kurtosis of \(X\) affects the standard error less. We should expect this, because the central limit-theorem tells us that \(Y\) approaches a normal distribution in the limit \(n \rightarrow \infty.\) Note that for zero excess kurtosis (\(\kappa_X = 3\)) the standard error of \(S_X\) does not depend on \(n\) anyway.

Volatility Estimates

---

Now imagine a process

$$Z_t = \sum_{i=1}^t X_i$$

Let’s say we sample this process every \(n\) time units, i.e \( Z_{jn}.\) The differences of this process give us back a series of iid realizations of \(Y:\)

$$Z_{(j+1)n} - Z_{jn} = \sum_{i=jn+1}^{jn+n} X_i \equiv Y_{j}$$

If we have observed up to time \(t = mn\) then we have \(m\) observations of \(Y,\) each consisting of the sum of \(n\) draws of \(X\). Thus, we can use \(S_X = S_Y / \sqrt{n}\) to estimate the volatility, and we can directly apply our formula equation \eqref{S_err_nm} to calculate the error on this estimate.

Effect of the Sampling Period

A natural question to ask is; for a fixed observation time, how does sampling frequency affect the accuracy of our estimate? The number of samples \(m\) is related to the total time \(t\) and sampling period \(n\) by \(m = t/n.\) Thus

$$\varepsilon = \frac{\Std{S_x}}{\sigma_X} = \sqrt{\frac{(\kappa_X - 3) + 2n}{4t}} \label{S_err_tn}\tag{5}$$

Firstly, let’s note that

$$\varepsilon \propto \frac{1}{\sqrt{t}}$$

So, as one might hope, sampling for a longer period always gives a better estimate. How about for the sampling period \(n?\)

Define \(c = (\kappa_X - 3)/2\). Remember \(\kappa_X \geq 1\) so \(c \geq -1,\) also note \(n \geq 1.\) Then we can write

$$\varepsilon \propto \sqrt{c + n}$$

Because the square-root function is monotonically increasing, this tells us it is always beneficial to reduce \(n,\) i.e. to increase the sampling frequency. In fact, because the square-root function is concave, the smaller \(n\) is, the greater the (relative) benefit in reducing it further.

However, as we increase the kurtosis, note that the overall benefit of increasing sampling frequency, decreases. This is because we move into a flatter part of the square-root curve. It should be clear visually, but you can also show it by calculating the gradient of \(\varepsilon\) wrt \(n\) and finding

$$\frac{\partial\varepsilon}{\partial n} \propto \frac{1}{\sqrt{c+n}}$$

Not only does increasing kurtosis decrease the benefit of sampling faster, it increases the errors we will see at the very fastest time-scales, for the same reason. As \(n\) tends to zero we do not approach zero error for positive excess kurtosis.

Effect of the Sample Count

We can similarly ask, still for fixed \(t,\) how the standard error scales with the number of samples. By substituting \(n = t/m\) into our formula above, and rearranging, we get

$$\varepsilon = \frac{1}{\sqrt{2}}\sqrt{\frac{c}{t} + \frac{1}{m}}$$

As above, from this it’s clear that increasing the sample count decreases the error but that we approach a non-zero error for an infinite number of samples and positive excess kurtosis.

We can also calculate the gradient of this wrt \(m,\) but it’s not as clean as the gradient wrt \(n,\) above. In this case, let’s do the following; say we have a number of samples \(m,\) what happens to the standard error if we increase (or decrease) this by a factor \(f,\) giving \(m^\prime = mf\)? We find

$$\frac{\varepsilon^\prime}{\varepsilon} = \sqrt{\frac{cm + 2t / f}{cm + 2t}}$$

For \(\kappa_X=3\) this gives \(\varepsilon^\prime/\varepsilon = 1/\sqrt{f}.\) This makes sense, \(f\) is directly related to the number of samples. The relative benefit of one more sample, in this case, is

$$\frac{\varepsilon - \varepsilon^\prime}{\varepsilon} = 1 - \sqrt{\frac{m}{m + 1}}$$

This follows because, for one extra sample, \(f = 1+1/m\). This function approaches zero as \(\sim m^{-1},\) i.e. as we get more samples the relative benefit of adding more drops away. (Though actually fairly slowly.)

If \(\kappa_X > 0\) then we find, for large \(m\), that the relative benefit instead goes as \(\sim m^{-2} / c\), meaning it drops off faster than in the mesokurtic case. Further, the higher the kurtosis, the smaller the benefit for each increase in sample count.

Despite this, the point above stands, it is always beneficial (at least mathematically) to sample more frequently. You may have other reasons that this becomes a trade-off; e.g. ability to fit your dataset in memory or something.

Empirical Verification

---

Let’s empirically test our formula to check it’s correct.

For a set time \(T\) we draw a realization of \(\{Z_t: t\leq T\}\), then for a given sampling period \(n\) we slice each realization into \(m = \lfloor T/n \rfloor\) samples and use \(S_X = S_Y/\sqrt{n}\) to estimate the volatility. We repeat this process until we have \(D\) estimates of our volatility, then calculate the empirical standard deviation of these estimates. We can compare this to our formula equation \eqref{S_err_nm}.

Repeating this for all sampling periods in the range \(1 \leq n < 150\) gives us a dataset we can plot:

We see that in the large \(m\) limit we get good agreement between equation \eqref{S_err_nm} and the observed values. (Remember, small \(n\) means higher frequency and so more samples.) As the sampling period increases, so \(m\) decreases and we start to see that the theoretical value is not such a good estimate. Here \(T = 1000\), therefore at the upper end of the graph we have only \(\lfloor 1000 / 150 \rfloor = 6\) samples. Unsurprisingly for such a small number our “large N” approximation breaks down!

Vortex Shedding

I have been working on my Lattice-Boltzmann simulation code recently. (Okay, given how long this article has been a draft, ‘recently’ is perhaps a stretch.) Simulating the vortex shedding of flow past a cylinder is practically a rite-of-passage for CFD codes. So let’s do it!

All the results shown here were produced with my code, which is available on GitHub. Specifically the script at vortex_street.py.

Setup

---

Flow Geometry

---

The flow setup (shown in the diagram) is a rectangular domain of height \(W\) and length \(L\). At the left and right ends in- and out-flow boundaries are enforced by prescribing that the velocity be equal to \(\mathbf u = (u, 0)\). The top and bottom boundaries are periodic. In the (vertical) centre of the domain is a circular wall boundary of diameter \(D\). Let’s define the y-axis such that \(y=0\) corresponds to the midline of our simulation.

This setup is called flow past a cylinder because we imagine the 2D simulation is a slice of a 3D system which is symmetric under translations in the z-direction.

Characteristic Scales

---

The suitable characteristic length-scale is the diameter of the cylinder \(D\), and the characteristic velocity is the prescribed in-flow velocity \(u\). Combined with the fluid’s kinematic viscosity - \(\nu\) - these give us the Reynold’s number

$$\mathrm{Re} = \frac{uD}{\nu}$$

The flow displays different behaviour depending on the value of \(\mathrm{Re}\). We can control this by changing any of \(u\), \(D\) or \(\nu\). In the simulations below I have done this by fixing \(D\) and \(\nu\) then inferring \(u\).

The characteristic timescale of the system is the time it takes the fluid to flow past the cylinder

$$T = \frac{D}{u}$$

We define the ‘dimensionless time’ to be \(\tau = t/T\). When comparing results across different Reynold’s numbers we will plot them at equal values of dimensionless time.

Flow Regimes

---

Depending on the Reynold’s number this setup displays 4 distinct behaviours.

Re.	Behaviour
<10	Creeping
10 - 100	Recirculation
100 - 1000	Vortex Shedding
> 1000	Turbulence

These ranges are only approximate. I have seen various figures quoted in different sources, for instance sometimes it’s stated that shedding starts at around Re = 40. In my results Re = 50 was stable for the whole simulation, unless I manually induced shedding by perturbing the initial velocity field.

Simulation

---

Initial Conditions

---

When setting up the simulation we could set the initial velocity to be equal to \(u\) everywhere. However, directly up- & downstream of the cylinder the velocities will be pointing respectively into, and out-of the wall boundary. This means, at these points, the velocity field is not divergence free.

At low velocities this causes a large “sound” wave to propagate outwards from the cylinder (compression at the leading edge and rarefaction at the trailing edge.) The velocities induced by this can be of similar order to the flow features we’re interested in. They will eventually propagate out of the domain but it’s needlessly ugly.

Here is what the initial disturbance looks likes for \(Re = 100:\)

The compression/rarefaction seen here is larger than 4%!

More problematically, at higher velocities (Reynold’s numbers) these pressure waves can even cause the simulation to become unstable and blow up. We have to do something better!

Stream Function

The initial pressure waves are mostly caused by the non-zero divergence of the velocity field. Therefore we can naturally think to start with a velocity field that is divergence free.

There are a few approaches we could try to get such initial conditions. One such is to construct a stream function, and to use this to get the velocity field. This works because stream functions exist only for divergence free flow fields, thus any velocity field derived from a stream function is guaranteed to be divergence free.

The stream function is a 2D scalar field - \(\psi\) - whose derivatives in each direction specify the velocity vector:

$$u_x = \frac{\partial \psi}{\partial y} \qquad u_y = -\frac{\partial \psi}{\partial x}$$

Because the velocity is specified by the gradients of \(\psi,\) it is not unique; any constant offset will yield the same velocity field.

A uniform velocity field $(u, 0)$, corresponds to stream functions of the form \(\psi_\text{uniform} = u y + C.\) Wlog. choose \(C = 0,\) so that the stream function is zero along the mid-line of our simulation. Next, we can notice that if the stream function’s gradients are zero at the cylinder walls then we have zero velocity here. Thus if we perturb \(\psi_\text{uniform}\) near the wall s.t. this is the case, we will get a velocity field which has the desired value far from the cylinder, tends to zero near the cylinder and is divergence free. Nice!

Obviously the stream function \(\psi = 0\) has zero gradient everywhere, and conveniently matches \(uy\) on the midline. So we can imagine interpolating between \(\psi = 0\) near the wall and \(\psi = uy\) far from the wall:

$$\psi = f(d)\cdot uy + \cancel{(1-f(d)) \cdot 0}$$

where \(d\) is the distance from the solid wall.

The interpolation function must have the following properties:

• \(f(\infty) = 1\) - One far from the walls.
• \(f(0) = 0\) - Zero near the walls.
• \(f^\prime(0) = 0\) - Zero gradient near the walls.

The last property is required because otherwise we would get a non-zero x-velocity at the wall:

$$u_x = \frac{\partial \psi}{\partial y}\bigg|_{d=0} = uy \partial_y f(0) + f(0)u$$

An obvious candidate is

$$f(d) = 1-e^{-(d/D)^2}$$

because \(e^{-x^2}\) has zero gradient at the origin. Moreover the gradient is actually linear around zero, which matches the expected velocity profile near a wall (see Wikipedia.)

Distance Function

To use calculate the stream function above we need to know the distance to our cylinder - \(d.\) This is very simple to calculate using the signed distance function for a circle. However, we can keep it more general by using the Euclidean distance transform. This lets us perform the same calculations for arbitrary geometries.

Here is an example of the stream function initial conditions applied to a semi-circular boundary:

Putting this together gives us the divergence free initial conditions for our simulation. The updated simulation start-up is shown below, with the same colour-scale as above:

The density fluctuations are much reduced, showing a maximum compression/rarefaction of under 1%. More importantly the simulation remains stable for higher Reynold’s numbers.

Density Initial Conditions

But why do we still see any density fluctuations? Ultimately it’s because the Lattice-Boltzmann method (LBM) solves for approximately incompressible flows.

In an incompressible fluid the pressure acts to keep the flow exactly divergence free. Fluid in the LBM is slightly compressible, with the pressure being related to the density via the equation of state

$$P = \rho c_s^2$$

But the flow is still almost incompressible so we expect corresponding pressure gradients, and these pressure gradients imply density gradients via the equation of state. Therefore, even without the initial transients, we will always see some density fluctuations in our LBM simulations.

We can use Bernoulli’s principle and the equation of state to relate the density to the velocity as

$$\frac{\rho}{\rho_0} = 1 - \frac{v^2 - u^2}{2c_s^2} \label{density_bernoulli}\tag{1}$$

Where I have used the fact that all streamlines in our initial velocity field end at the in-flow boundary, letting us fix the constant in Bernoulli’s relation. \(\rho_0\) is the arbitrary density at the in-flow.

We can use equation \eqref{density_bernoulli} to set the initial condition for the density. Even doing this, however, we would still expect some initial transients. This is because the stream function we used is arbitrary (up to the constraints), and is not a solution to the Navier-Stokes equation (probably).

Surprisingly, I found that setting the initial density in this way actually made the transients marginally worse. Therefore, for my simulations I have simply let the density be uniform throughout the domain.

Plotting

---

Choosing Colour-scales

In order to accurately compare the results across different Reynold’s numbers it is important for the colour-scales to match. All the results shown here have a velocity magnitude colour-scale from 0 to \(2u\), and a vorticity colour-scale from \(-50u/D\) to \(+50u/D.\) These numerical prefactors were determined empirically to give useable scales.

Streamlines

When visualizing flow fields the streamlines can be a useful addition, even for time varying flows. One difficulty with plotting them, is choosing the seed points from which to integrate the velocity field. For example, if we choose some seed points at the inflow boundary, then we will not see any streamlines in the recirculation regions behind the cylinder. To get around this we can actually make use of the stream function again.

The contours of the stream function correspond to the stream lines of the velocity field. Therefore if we calculate the stream function, we can easily plot streamlines including in disconnected parts of the flow. (This is going the other way from the initial conditions where we went from the stream function to the velocity.)

One definition of the stream function is that it is the flux through any path from a reference point to the current position. This is given by the line integral

$$\psi(\mathbf x) = \int_{\mathbf x_\mathrm{ref}}^{\mathbf x} \mathbf v \cdot \hat{\mathbf n} \,dl$$

Because the exact path is not important we can arbitrarily say we will take a path which goes first vertically, and then horizontally from \(\mathbf x_\mathrm{ref}\) to \(\mathbf x.\) Thus the integral becomes

$$\psi(\mathbf x) = \int_{y_\mathrm{ref}}^y v_x dy + \int_{x_\mathrm{ref}}^x v_y dx$$

which is something we can easily calculate numerically.

It is important to note that although \(\mathbf x_{\mathrm{ref}}\) does not affect the velocity field we would get back from the \(\psi\), it obviously affects the value of \(\psi\) itself. We need our contour levels to be consistent over time, so we need to choose a reference point whose velocity does not change. I have used the lower-left corner, which is in the inflow boundary and thus has velocity fixed at \(u.\)

Results

---

This section shows the results of the simulation for various Reynold’s numbers, at a late dimensionless time \(\tau=100.\) This is enough time to let the initialization effects fully propagate out of the domain, and for the flow to establish its long-time behaviour. The chosen Reynold’s numbers display the four regimes mentioned above; creeping flow, recirculation, vortex shedding and, finally, turbulence.

The simulations for Reynold’s number 5 and 50 have domains with grid sizes 1000 × 3000, i.e. 3 million cells. The higher Reynold’s numbers require a higher resolution and so were run at 4000 × 12,000, i.e. 48 million cells.

If you’re interested in seeing the time evolution you can head over to YouTube, for a video showing the simulation for Re = 500 and Re = 5000. Re = 5 and Re = 50 are not worth a video since they settle into a steady-state!

Cylinder Frame

First, let’s look at the fluid velocity (magnitude) in the rest frame of the cylinder. This is how the simulation is actually run, and matches the set-up described above with in- and out-flow boundary conditions.

We can see, as expected, the four flow regimes for the different Reynold’s numbers.

For Re \(<\) 100 we see that, after the initial transients have advected out of the domain, the flow settles into a steady-state with no vortex shedding. In both cases there is a region of “stagnant” flow trapped just behind the cylinder, which has zero net velocity.

For Re = 50, if we look closely, we can see a slight non-zero velocity along the midline in the middle of this stagnant region. In fact, the velocity is not only non-zero, it is heading in the direction opposite to the bulk flow! This is because the flow is recirculating. It’s hard to see when looking at the whole domain and with the chosen colour scale, though, so let’s look a zoom of just the recirculation region.

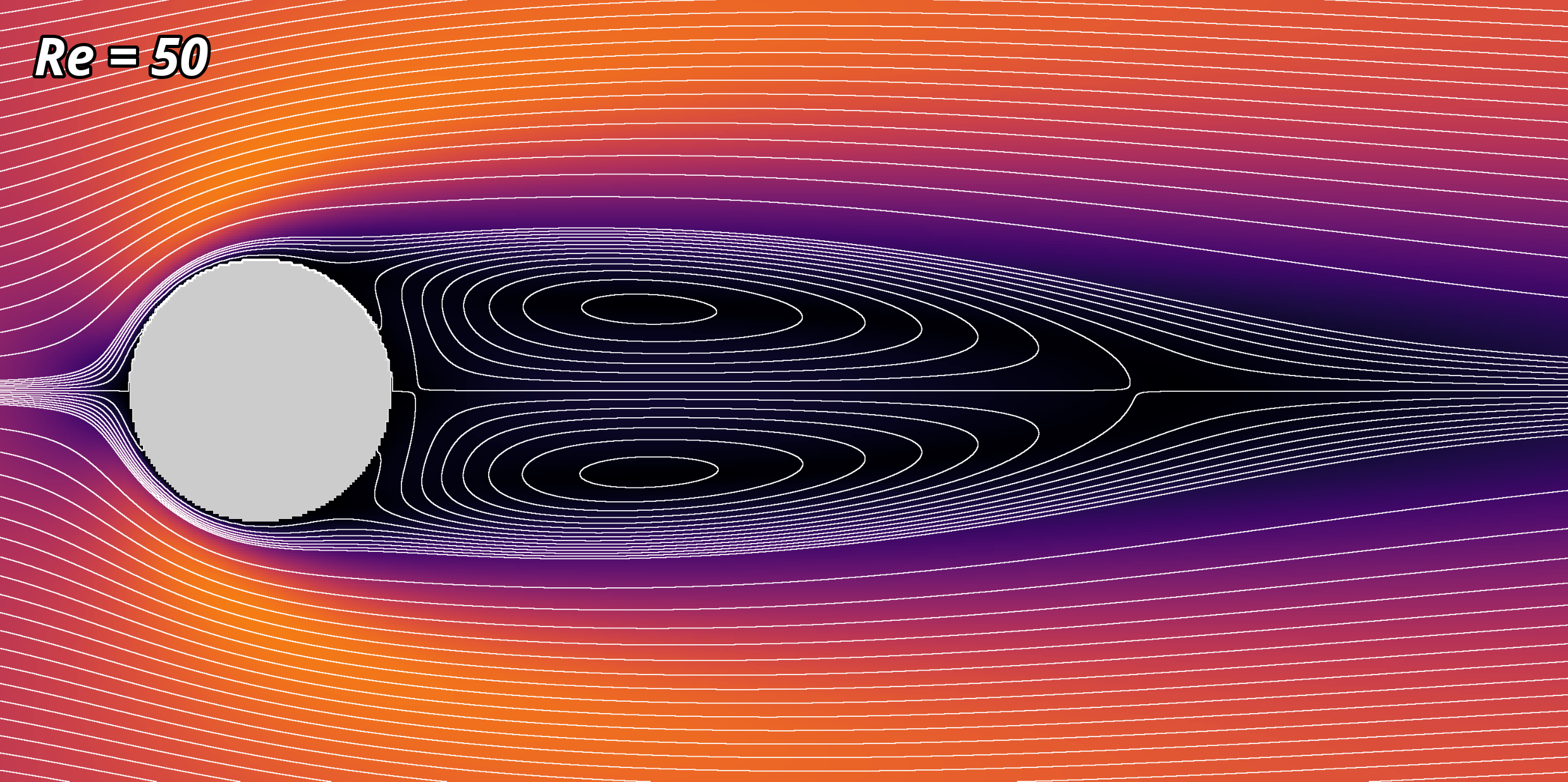
Here I have not blended the streamlines with the velocity field, as above, but just overlain them directly to make them more visible. Because the simulation is steady-state for Re = 50, the streamlines do correspond to pathlines of the flow, and we see that just downwind of the cylinder they are closed loops. This means that fluid is trapped, and being pushed around in a vortex motion, i.e it is recirculating.

At higher Reynold’s numbers the recirculation zone grows, and eventually becomes unstable. First one of the recirculation vortices is shed, then while it reforms the the other is shed, etc. When looking at the plot for Re = 500 above, however, it is not obvious that the periodic flow feature behind the cylinder is a sequence of vortices. The flow is not steady-state, so the streamlines do not correspond to path- or streaklines of the flow. Despite that, the fact they are not closed here doesn’t make them look much like a vortices. This can be remedied by considering the fluid’s own rest-frame.

Fluid Frame

Instead of considering the cylinder fixed, and the fluid as flowing past it with velocity \(u\), we could equally well consider the fluid as being fixed and the cylinder moving through it with velocity \(-u.\) This is the ‘fluid frame’. The fluid frame velocity is given by \(v_x^\prime = v_x - u\) and \(v^\prime_y = v_y,\) and the magnitude is correspondingly changed.

In this frame we see that for Re = 5 and Re = 50, the stagnant region behind the cylinder is, instead, an entrained pocket of fluid. For the fluid rest frame the streamlines do not coincide with the pathlines even for Re = 5 and Re = 50, because in this frame cylinder is viewed as moving, therefore the flow cannot be steady-state.

For Re = 500 and Re = 5000, despite the flow also not being-steady state, the streamlines do form closed loops behind the cylinder, showing that we have formed vortices.

At Reynold’s number 500 they form a regular line, with each vortex rotating in the opposite sense to its neighbours. The vortices are not moving relative to the surrounding fluid, the non-zero velocity in this reference frame purely shows their rotation. Although it is tempting to think it looks like the entrained fluid pocket for lower Reynold’s numbers, it is not. The high velocity in the band behind the cylinder is actually perpendicular to the cylinders motion. Picture the cylinder moving through stationary fluid, leaving a line of vortices, whose centers are stationary, in its wake.

By the time we get to Re = 5000, turbulence has set in and they shoot off in random directions, and tend to form pairs of oppositely rotating vortices. If you watch the video, you can even see that these sometimes collide and the pairs swap vortices.

From the velocity magnitude + streamlines we cannot tell which way the vortices are rotating. This, we can visualize with the vorticity.

Vorticity

The vorticity is given by the curl of the velocity field: \(\nabla\times\mathbf v.\) It is unchanged by a constant offset of the velocity

$$\boldsymbol{\omega}^\prime = \nabla\times\mathbf v^\prime = \nabla\times(\mathbf v + \mathbf u) =\nabla\times\mathbf v + \nabla\times\mathbf u = \nabla\times\mathbf v = \boldsymbol{\omega}$$

because for a constant vector \(\nabla\times\mathbf u = 0.\) Therefore, it does not matter if we take the curl of the cylinder-frame or the fluid-frame velocity field.

Orange shows positive vorticity (i.e. anticlockwise rotation) and blue, negative vorticity (clockwise rotation).

Mechanisms

---

Creeping Flow

---

At very low Reynold’s numbers, creeping flow shows neither time evolution, nor eddies. In this regime the flow is governed by Stokes equations, which does not have any time dependence. Its inertia is so weak compared to viscosity, that it instantly responds everywhere to the boundary conditions.

Recirculation

---

For slightly higher Reynold’s numbers the approximation behind Stokes flow, that viscosity completely dominates inertia, starts to break down and we do get eddies forming.

These are formed behind the cylinder by flow separation. As the fluid flows past the cylinder it is at first constricted, which means the velocity must increase (mass conservation) and thus the pressure decreases (Bernoulli’s principle). Once past the midpoint, however, the channel becomes less constricted again and the velocity drops, and thus the pressure increases. The overall flow is therefore going against the pressure gradient at this point. Near the boundary the flow is slower, so this adverse pressure gradient actually causes the flow here to reverse, and go against the bulk flow, causing the eddies.

An obvious question to ask is why is the recirculation stable for these intermediate Reynold’s numbers? Why do we not see vortices being shed here? Unfortunately I could not find a good answer in the literature. (One must exist, surely?)

If I were to hazard a guess I’d say that, although we now have recirculating eddies, the flow is still viscous enough that the bulk behaves more-or-less like Stokes flow. Disturbances in the flow are felt quickly far away via the rapid diffusion of momentum associated with the high viscosity. The bulk flows around the combined “cylinder + eddies” obstacle, which “deconstricts” more gently than the cylinder alone, thereby ameliorating the adverse pressure gradient for the bulk. (One obvious feature of this interpretation is that, although the cylinder has no-slip boundary conditions, the eddies most certainly do not. But perhaps that does not matter.)

Shedding

---

I think the exact cause of the vortex shedding is not currently well understood. At least, that’s what’s stated in the abstract of nearly every paper I looked at whilst trying to understand the mechanism(s) involved in vortex shedding. Many papers investigating vortex shedding are numerical, rather than theoretical, and examine simulations in fine detail. While useful, I was looking for something more mathematical.

I found this paper by Boghosian & Cassel quite nice; it is at the same time sufficiently mathematical and quite readable. It examines under which situations vortices in 2D incompressible flow split. The gist of the paper is that at points of zero momentum, having \(\nabla\cdot\frac{d\mathbf u}{dt} > 0\) will cause a vortex to split. While I like the paper, I don’t think it explains the vortex shedding mechanism observed here. They show that for a general vortex the pressure gradient is not enough to get the divergent net force, so they need to add a body force. That is clearly not the situation we have here.

A common suggestion for the cause of vortex shedding, which seems sensible to me, is a form of Kelvin-Helmoltz instability.

The fluid-frame velocity magnitude plots for Re = 50 show how we have two shear layers just downstream of the cylinder; one extending from the top, and one from the bottom. This is true in the early flow for higher Reynolds numbers too. Because of the Kelvin-Helmholtz instability, this shear layer is unstable and will naturally form growing vortices.

This makes sense but it cannot be the whole story; the shear layer exists also for lower Reynold’s numbers, and according to theory, shear layers are always unstable (if the densities of the fluid on either side are equal.) This is the flip-side of the question of why the recirculating vortices are stable for low Re; why do they become unstable for higher values of Re?

von Kármán Vortex Street

---

But wait, what about the famous von Kármán Vortex Street? This is the famous effect whereby vortices shed behind an obstacle create two rows of opposite rotational sense, between which the vortices are offset from one another. This is beautifully illustrated in this satellite image from NASA:

Consider two rows of vortices separated by a distance denoted \(h\), with each row containing vortices rotating in opposite directions. Within each row let the distance between vortices be denoted by \(l\). According to von Kármán’s analysis, any arrangement apart from \(\frac{h}{l} = \frac{1}{\pi}\mathrm{arcosh}(\sqrt{2})\approx0.28\) is unstable.

However, my simulations did not show this predicted, and rather beautiful, pattern. Instead, the vortices form a single line of alternating sense along the midline. Why?

I think the answer, ultimately, comes down to boundary conditions. I ran the simulations with a larger domain and I do see the predicted offset vortices:

The vortices have been visualized here by letting two tracers (dyes) advect with the fluid; the top half of the obstacle releases red dye, and the bottom green. Where these mix it creates yellow, but you can clearly see the red & green dye trapped in the vortices being carried off downstream.

This simulation was run at Re = 100. In the simulations I ran, at lower Reynold’s number the von Kármán pattern developed closer to the obstacle. For higher Reynold’s numbers it did develop, just somewhat downstream of the obstacle. However, with the original shorter geometry, even at Re = 100 the vortices formed a line, rather than the von Kármán pattern.

Consider the velocity field formed by the vortex street arrangement, in the rest frame of the bulk fluid. I will describe it with words, but to aid the subsequent description, let’s just look at it:

Between neighbouring pairs of opposite sense vortices the fluid flows fast, and on the outer edges of the vortices, slowly. Thus fluid between the two rows is, on average, moved to the left (for our configuration). The vortices themselves “roll” between this moving central fluid, and the stationary bulk fluid. This rolling causes some slight rightward motion of the bulk fluid just outside the vortex street.

If we imagine averaging the fluid’s velocity over time we get the right-hand side of the above figure. This clearly shows how the fluid behind the cylinder is entrained and has non-zero velocity.

This is the reason, then, I believe the boundary conditions are affecting the vortex street formation. For the vortex street, the velocity profile along a vertical slice is anything but uniform and steady-state. By contrast, our boundary conditions set a uniform and constant velocity across the whole right-hand edge.

Because the vortex street has a leftward velocity relative to the velocity at our boundary, it is forced to accelerate as it exits the domain. This has the effect of pulling the vortices inwards. Additionally (and perhaps more importantly?) the constant velocity outflow condition kills any rotational motion as the flow approaches the boundary.

This suggests an interesting test would be to implement some more sophisticated boundary conditions, e.g. non-reflecting / characteristic boundary conditions, which will let the vortices flow out of the system unimpeded.

References

---