The Lattice Boltzmann Method - Theory
Here I’ll show the theory behind simulating the Boltzmann equation in 1d using the lattice Boltzmann method. There’s nothing particularly special about 1d, but it removes some notational burden and removes some minor complexities which are not important for understanding the method.
Contents
Collision Operator
The Boltzmann equation in 1d is
$$\frac {\partial f} {\partial t} = \Omega f - q\frac{\partial f}{\partial x} - \frac{F}{\rho}\frac{\partial f}{\partial q}$$Before we can make any progress we need to define the collision operator $\Omega$. The exact form of $\Omega$ involves some modelling choices, but clearly it should obey some constraints
- Mass conservation - Particles should be neither created nor destroyed.
- Momentum conservation - The total linear momentum should remain unchanged.
- Energy conservation - The total kinetic energy should not change.
The simplest collision operator which is used in practice is the Bhatnagar, Gross and Krook (BGK) operator. After the atoms in our gas have collided many times they will come to equilibrium. The BGK collision operator simply relaxes all velocities towards their equilibrium values exponentially with a set timescale $\tau$
$$\Omega_\mathrm{BGK}(f) = \frac 1 \tau \left(f^\mathrm{eq}(\mathbf q) - f(\mathbf q)\right)$$where the equilibrium distribution - $f^\mathrm{eq}$ - is the local Maxwell distribution. Note, I have elided the dependence of $f$ on $t$ and $\mathbf x$ for clarity here and throughout.
If $f^\mathrm{eq}$ has the same moments as $f$, then linearity of integration means that the moments are conserved by the BGK operator.
$$\begin{align} \int (\Omega f) q^k dq &= \frac{1}{\tau}\int\big(f^\mathrm{eq}(q) - f(q)\big) q^k dq \\ &= \frac{1}{\tau}\Big(\int f^\mathrm{eq}(q) q^k dq - \int f(q) q^kdq\Big) \\ &= 0 \end{align}$$This means our goal will be to find a numerical scheme which lets us write the equilibrium distribution such that its moments exactly match the non-equilibrium distribution.
Equilibrium Distribution
What is the distribution of velocities at equilibrium? Well, the distribution of speeds is given by the famous Maxwell-Boltzmann distribution . This is the distribution of the magnitude of a 3d Gaussian distribution, with zero mean and covariance matrix $\sigma^2 \mathbf I$ where
$$\sigma^2 = \frac{k_BT}{m}$$with $m$ - the particles’ mass, $k_B$ - Boltzmann’s constant, and $T$ the temperature. In our case we have a 1d system and so we expect a 1d Gaussian with zero mean and variance given by the above. Great.
One may ask, but why is the result a Gaussian with that variance? Well, at equilibrium we can expect the distribution of velocities to be at maximum entropy. Given a specified mean and variance the maximum-entropy distribution is the Gaussian (see Wikipedia ). The value of variance itself comes from the average kinetic energy of our particles. The Equipartition theorem tells us that, at equilibrium, the internal energy is equally distributed amongst all the degrees of freedom of the gas. For the translational degrees of freedom, the internal energy corresponds to the kinetic energy of the particles, and is related to temperature by
$$ \frac{k_BT}{2} = \langle \frac{1}{2}mq_\alpha^2\rangle = \frac{1}{2}m\,\mathbb \langle q_\alpha^2\rangle = \frac{1}{2}m\sigma^2 $$which gives
$$\sigma^2 = \frac{k_B T}{m}$$as above.
If there is a net macroscopic velocity $u$ then the equilibrium distribution becomes a Gaussian with mean $\mathbf u$ and the same variance as above;
$$\mathbf q^\mathrm{eq} \sim \mathcal N\left(\mathbf u,\, \frac{k_BT}{m}\mathbf I\right)$$In 1d the equilibrium distribution function is then
$$f^\mathrm{eq}(q) = \rho\sqrt{\frac{m}{2\pi k_B T}} \exp\left(-\frac{m}{2k_B T}(q-u)^2\right)$$To get the temperature we can just use
$$T = \langle \frac 1 2 m (q - u)^2\rangle = \frac{1}{2} \int (q - u)^2f(q)\,dq$$remembering that $f^\mathrm{eq}(q)$ and $f(q)$ gives us the total mass density of particles with velocity $q$. To simplify, denote
$$\theta:=\frac{k_B T}{ m}$$making the equilibrium distribution
$$f^\mathrm{eq}(q) = \frac{\rho}{\sqrt{2\pi\theta\,}}\exp\left(-\frac{(q - u)^2}{2\theta}\right) = \frac{\rho}{\sqrt\theta} \,w\left(\frac{q-u}{\sqrt\theta}\right)$$where $w(q) = e^{-\frac{q^2}{2}} / \sqrt{2\pi}$ is the PDF of a standard Gaussian.
Simulation Setup
As a first attempt to make a numerical scheme we might just to discretize time, space and velocity directly, and consider the value of $f$ on a grid in phase space and time. Let’s say that our grid spacings in $t$, $x$ and $q$ are $\Delta t$, $\Delta x$ and $\Delta q$ respectively. And we denote the point $(t\Delta t, x\Delta x, q\Delta q)$ by its indices into the grid $(t, x, q) \in \mathbb Z^3$.
The outline for our scheme is as follows:
- Advect / Stream - For each point in the phase space grid, shift its value of $f$ along the requisite number of cells in the $x$ direction.
- Calculate - Calculate the new macroscopic moments at each point
- Infer - Infer the local equilibrium distribution.
- Collide - Perform the BGK collision operation.
Consider the first step; at a given value of velocity $q\Delta q$ the distribution function will be advected a distance $q\Delta q\Delta t$ in one timestep. In order that the advected distribution function lands back on our grid after one timestep we require $\Delta q = \Delta x / \Delta t$. This means that in “lattice units” the velocities are always just an integer $q$, and the values of $f$ with lattice velocity $q$ in phase-space just gets shifted $q$ lattice points along. Mathematically this can be written $f(t+1, x, q) = f(t, x - q, q)$ which is familiar from the article where we derived the Boltzmann equation.
For the second step, lets do the obvious thing and just approximate the moments with a finite sum
$$\mathbb E[Q^k(t, x)] \approx \sum_{q=-N}^{N} f(t, x, q) (q\Delta q)^k$$Then we can calculate the value of the equilibrium distribution at each point in phase space using the analytical form above
$$f^\mathbf{eq}(t, x, q) = \frac{\rho(t, x)}{\sqrt{\theta(t, x)}}w\left(\frac{q\Delta q - u(t, x)}{\sqrt{\theta(t, x)}}\right) $$Once we have calculated the equilibrium distribution, the last step is simple. For each point in our phase-space grid we just perform the BGK collision
$$\begin{align} f(t+1, x, q) &= f(t, x, q) - \Omega(t, x, q)\\ &= f(t, x, q) - \omega \big(f(t, x, q) - f^\mathbf{eq}(t, x, q)\big) \\ &= (1 - \omega)\,f(t, x, q) + \omega\, f^\mathrm{eq}(t, x, q) \end{align}$$where $\omega = {\Delta t}/{\tau}$.
This scheme will work (kind of). You can code it up and run some simulations and you’ll see things happening. But pretty quickly you’ll notice that our precious fluid is leaking away! Where’s it going? Ultimately, the problem is that our calculation of the moments is only approximate.
Imagine a completely quiescent fluid, the distribution function should be at equilibrium, so $f = f^\mathrm{eq}$ and nothing should be happening. But, with our current scheme we will get a slightly incorrect estimate for the density, and thus our inferred values for $f$ will be subtly different from the original values. This means at the next timestamp, when we calculate the density again, we will get a different value from in the pervious timestep. This cycle repeats, and after a few steps our moments have drifted wildly.
If we really increase the velocity resolution (decrease $\Delta q$) we can get a better and better approximation, but this means we need to reduce $\Delta x$ and $\Delta t$ commensurately, and the simulation will take longer and longer. Increasing the resolution is just a sticking-plaster, over long times our simulation will still be inaccurate due to non-conservation of the macroscopic moments.
What we need, therefore, is a velocity discretization scheme which lets us exactly calculate our moments. Fortunately such a scheme exists, and as we shall see we can represent the macroscopic moments we care about with just three velocities!
Gauss & Hermite to the Rescue
Hermite Series Expansion
Certain functions can be expanded using the Hermite polynomials as a basis:
$$f(q) = w(q)\sum_{n} \frac{a_n}{n!} H_n(q)$$The coefficients - $a_i$ - are given by
$$a_i = \int f(q) H_i(q)\,dq$$and the first three (probabilist’s) Hermite polynomials are
$$\begin{align} H_0(q) &= 1 \\ H_1(q) &= q \\ H_2(q) &= q^2 - 1\\ &\dots \end{align}$$Let’s expand our equilibrium distribution in this way and see what we get. Its first few Hermite coefficients are
$$\begin{align} a^\mathrm{eq}_0 &= \rho \int \frac{1}{\sqrt\theta} \,w\left(\frac{q-u}{\sqrt\theta}\right) dq = \rho \\ a^\mathrm{eq}_1 &= \rho\int \frac{1}{\sqrt\theta} \,w\left(\frac{q-u}{\sqrt\theta}\right) \,q\, dq = \rho u\\ a^\mathrm{eq}_2 &= \rho\int \frac{1}{\sqrt\theta} \,w\left(\frac{q-u}{\sqrt\theta}\right) \,(q^2 - 1)\, dq = \rho (u^2 + \theta - 1)\\ \end{align}$$The first two are just the zeroth & first moments of a normal distribution, so the result is clear. The third is a linear combination of the second non-central moment and the zeroth moment.
So, the Hermite expansion of our equilibrium distribution involves only the macroscopic moments we are interested in. Nice! If we truncate the the series with just these three terms we get
$$\begin{align} f^\mathrm{eq}(q) &\approx f^\mathrm{eq}_2(q) = w(q)\rho\left(1 + uq + \frac{1}{2}(u^2 + \theta-1)(q^2 - 1)\right) \end{align}$$Here we have an approximate representation of our equilibrium distribution $f^\mathrm{eq}(t, x, q)$, but it is still continuous in both space and velocity. Plotting the sum of the first few terms in the expansion, we can see how it approaches the true equilibrium distribution. Here the values of $\rho$, $u$ and $\theta$ have been chosen arbitrarily for illustrative purposes.
The $n$-th order approximation to the equilibrium distribution has the same first $n$ moments as the full distribution. This can be proved quite easily.
Let us consider the $k$-th moment, where $k\leq n$. Any monomial $q^k$ has itself a Hermite series expansion
$$q^k = \sum_{i=0}^{m} b_i H_i(q)$$for some coefficients $b_i$, whose values are not important for the proof, and $m = \lfloor k/2\rfloor$ which, crucially, is less than $k$ and thus $n$. Thus
$$\begin{align} \mathbb E[Q^k] &= \int_\mathbb R f^\mathrm{eq}_n(q)\, q^k\,dq\\ &= \int_\mathbb R w(q) \left(\sum_{i=0}^n a_i H_i(q)\right) \left(\sum_{j=0}^m b_j H_j(q)\right) dq &\quad\text{Series expand}\\ &= \int_\mathbb R w(q) \left(\sum_{i=0}^\infty a_i H_i(q)\right) \left(\sum_{j=0}^m b_j H_j(q)\right) dq & \quad\text{Orthogonality}\\ &= \int_\mathbb R f^\mathrm{eq}(q) \,q^k\,dq \end{align}$$We can let $n\rightarrow \infty$ here without affecting the result because the $H_i$ are orthogonal, and so the extra cross terms that arise from increasing $n$ are identically zero. But if $n=\infty$ then we recover the full equilibrium distribution, and therefore the moments must match.
In reality the fact the expansion only involves the first few moments of our equilibrium distribution should not be surprising. The definition of $a_i$ and the fact that the Hermite polynomials are, well, polynomials means this will be true for any distribution. So why is this a useful approximation?
Gauss-Hermite Quadrature
The real beauty of using the Hermite expansion for a Gaussian distribution is that we can use the so-called Gauss-Hermite quadrature to ensure exact conservation of our moments, even with a finite sum.
Gauss-Hermite quadrature is a form of Gaussian quadrature , which lets us re-write certain integrals as finite sums. Specifically
$$\int_\mathbb R w(q)\,P_k(q)\,dq = \sum_{i=1}^n w_i P_k(q_i) \qquad 2n-1\geq k$$where $P_k$ is any $k$-th order polynomial, and the weights - $w_i$ - and abscissae - $q_i$ - are pre-determined by the roots of $H_n$, the $n$-th Hermite polynomial.
Notice that the integrand on the left looks a lot like our approximation for $f^\mathrm{eq}$:
$$ f^\mathrm{eq}(q) \approx w(q)\,\underbrace{\rho\left(1 + uq + \frac{1}{2}(u^2 +\theta-1)(q^2-1)\right)}_{:=F_2(q)} $$Where $F_2(q)$ is a second degree polynomial in $q$. Thus if we want to calculate the $k$-th moment we can write
$$\begin{align} \int_\mathbb R f^\mathrm{eq}(q) \,q^k\,dq &= \int_\mathbb R w(q) \,F_2(q)\,q^k\,dq \\ &= \sum_{i=1}^n w_i F_{2}(q_i)\,q_i^k & \text{with }n\geq (k+3)/2 \end{align}$$The last equality holds because $F_2(q)$ is a second degree polynomial in $q$, which means $F_2(q)q^k$ is a $(k+2)$-th degree polynomial, and therefore we can apply the Gauss-Hermite quadrature rule. If we choose $2n-1 \geq k + 2 \Rightarrow n \geq (k + 3) / 2$ we can exactly represent our moments, otherwise it is just an approximation. If we wish to exactly reproduce up to the second moment we should therefore choose $n = 3$.
Thus our velocity discretized equilibrium distribution is given by
$$f^\mathrm{eq}_i = w_i F_2(q_i) = w_i \rho\left(1 + uq_i + \frac{1}{2}(u^2 +\theta-1)(q_i^2-1)\right)$$which is just part of the summand in the Gauss-Hermite rule above.
Note that the discretized equilibrium distribution approximation has the Gauss-Hermite weights baked in so they do not need to be considered when calculating moments as a finite sum, e.g.
$$\rho u= \sum_{i=1}^n f^\mathrm{eq}_i q_i = \int_\mathbb R f^\mathrm{eq}(q) \,q\,dq$$Our discretized approximate equilibrium distribution depends on it’s moments. This is not circular because the moments are determined by the non-equilibrium distribution, and by discretizing in this very specific way we ensure that our implied discrete equilibrium distribution has exactly the same moments.
For a while I was hung up on wondering why we even need to expand the equilibrium distribution using the Hermite series. Afterall, our equilibrium distribution looks like an exponential of minus something squared. So we should be able to transform it such that the moment integrals become suitable for Gauss-Hermite quadrature. Indeed we can. If we just standardize our equilibrium distribution via the change of variable $q^\prime = (q - u)/\sqrt{\theta}$, we can directly apply Gauss-Hermite quadrature and calculate the moments exactly.
$$\begin{align} \rho\int_\mathbb R \frac{1}{\sqrt\theta} w\left(\frac{q-u}{\sqrt{\theta}}\right)q^k\,dq &= \rho\int_\mathbb R w(q^\prime) (\sqrt\theta q^\prime + u)^k \,dq^\prime \\ &= \rho\sum_{i=1}^n w_i(\sqrt{\theta}q_i^\prime + u)^k \end{align}$$But this doesn’t help us; we already know the moments, since they are specified by the non-equilibrium distribution. Indeed they are required for the change of variables. (Oh look, all three first moments appear in the moment calculation!)
Ultimately what we are after is the value of the equilibrium distribution $f_i^\mathrm{eq}$ on our finite velocity set so that we can apply the collision operator, while still obeying the required conservation laws! To get this we need to use the Hermite expansion, which gives us the approximation already in the form $w(q)F_2(q)$, no change of variables required.
D1Q3 Velocity Set
So, we’ve shown that we can achieve exact conservation of moments, even with a discretized velocity set. Great!
The size of said set determines the highest moment we can represent exactly. Since we (typically) only care about the variance ($k=2$) a set of size $n=3$ will suffice. The values for $q_i$ and $w_i$ are completely predetermined and have nothing to do with our set-up, they are
| $i\vphantom{\frac{1}{6}}$ | $0$ | $1$ | $2$ |
|---|---|---|---|
| $w_i$ | $\frac{4}{6}$ | $\frac 1 6$ | $\frac 1 6$ |
| $q_i\vphantom{\frac{1}{6}}$ | $0$ | $\sqrt{3}$ | $-\sqrt{3}$ |
Such velocity sets are labelled by the spatial dimension and size via the nomenclature DxQy, so here we are using the D1Q3 velocity set.
For the simulation we want our velocities to align with our lattice so our lattice spacings must actually be $\sqrt 3$ apart. This means that 1 “lattice unit” is equivalent to $\sqrt 3$ “raw units”. If we rewrite our velocity set to be in lattice units we need a conversion factor. We will denote the velocity set in lattice units by $c_i$ and in raw units by $q_i$ then we have
$$c_i = \frac{q_i}{\sqrt 3}$$If we denote the conversion factor as $c_s = \frac{1}{\sqrt 3}$ then $q_i = c_i / c_s$, thus the moments (in raw units) are given by the following
$$\sum_{i=1}^n f_i q_i^k = \frac{1}{c_s^k}\sum_{i=1} f_ic_i^k$$So, for example the mean velocity calculated in raw units becomes
$$\rho u_\mathrm{raw} = \sum_{i=1}^n f_i q_i = \frac 1 {c_s} \sum_{i=1}^n f_i c_i = \frac {\rho u_\mathrm{lat}}{c_s}$$Note that the zero-th moment does not change. Re-writing our equilibrium distribution gives
$$f^\mathrm{eq}_i = w_i \rho\left(1 + \frac{u_{\mathrm{lat}}c_i}{c_s^2} + \frac{1}{2}\left(\frac{u_\mathrm{lat}^2}{c_s^2} + \frac{\theta_\mathrm{lat}}{c_s^2} - 1\right) \left(\frac{c_i^2}{c_s^2}-1\right)\right)$$It is cumbersome to carry around the ‘$\mathrm{lat}$’ subscript everywhere so you will almost always see this written with just $u$ instead, and the mean calculation given just as
$$\rho u = \sum_{i=1}^nf_ic_i$$This is completely consistent with what we have derived, but can make the appearance of the factors of $c_s$ seem a bit magical. Additionally, one must take care about whether any velocities are in lattice or raw units. The notation $c_s$ is suggestive of a speed-of-sound, and indeed it can be shown that it corresponds to the speed of sound in our simulations.
Isothermal assumption
In real gases, macroscopic flow features can cause local adiabatic heating and cooling, and so $\theta$ may vary from place-to-place and over time. However, we run into a problem using D1Q3. We have three discrete distribution values and three moments to represent, thus the system is completely constrained. The implied equilibrium distribution for D1Q3 must always just be exactly equal to the non-equilibrium distribution. As much as that sounds like a contradiction, we can check that it is actually the case numerically;
import numpy as np
from numpy.polynomial.hermite import hermgauss
# get D1Q3 velocities & weights
q, w = hermgauss(3)
# convert from physicist's to probabilist's scaling
q *= np.sqrt(2)
w /= np.sum(w)
# draw any old non-equilibrium distribution
f = np.random.exponential(size=3)
# calculate moments
m0 = np.sum(f)
m1 = np.sum(f * q) / m0
m2 = np.sum(f * (q - m1) ** 2) / m0
# imply equilibrium distribution
feq = w * m0 * (1 + m1 * q + 0.5 * (m1**2 + m2 - 1) * (q**2 - 1))
# hmm moments match ...
eps = 1e-8
assert abs(m0 - (np.sum(f))) < eps
assert abs(m1 - (np.sum(f * q) / m0)) < eps
assert abs(m2 - (np.sum(f * (q - m1) ** 2) / m0)) < eps
# oh, the distributions are actually identical!
assert all(np.abs(feq - f) < eps)
Here we’ve used the helpful Numpy function hermgauss to get the weights & abscissae.
It doesn’t matter how many times you run this code, none of the assertions will ever fail!
So what? Well, if our implied equilibrium distribution is always exactly equal to our non-equilibrium distribution our collision operator is not doing much, is it? If the collision operator is doing nothing we are effectively simulating the pure advection case.
For this reason in we will make the so-called isothermal assumption. This is nothing more than saying, that the temperature is equal everywhere, regardless of what the fluid flow is doing. Therefore we can choose $\Theta(t, \mathbf x) = c_s^2$ (in lattice units) and our equilibrium distribution simplifies somewhat to
$$f^\mathrm{eq}_i = w_i\rho\left(1 + \frac{u c_i}{c_s^2} + \frac{1}{2}\frac{u^2}{c_s^2} \left(\frac{c_i^2}{c_s^2}-1\right)\right)$$We can simplify further if we notice $c_s^{-2} = 3$ which gives
$$f_i^\mathrm{eq} = w_i \rho\left(1 + 3uc_i -\frac{3}{2}u^2+ \frac{9}{2}u^2c_i^2 \right)$$If we want to model the thermal aspects of the flow we can either
- extend the velocity set to give us more degrees of freedom,
- or explicitly model the advection-diffusion of heat, and couple it to the fluid motion through something like the Boussinesq approximation .
Lattice Boltzmann Method
Putting all the steps together we arrive at the Lattice Boltzmann Method. Our exact simulation method is pretty much the steps detailed above, just with our Gauss-Hermite D1Q3 velocity set and the nice Hermite series approximation for the equilibrium distribution.
- Advect / Stream - For point $(x, q)$ shift the value of $f$ to $(x+q, q)$.
- Calculate - Calculate the new macroscopic moments at each point as simple finite sums.
- Infer - Infer the local equilibrium distribution using our $f_i^\mathrm{eq}$ in lattice-units.
- Collide - Perform the BGK collision operation.
I have written a very simple simulation using this scheme in Numpy.
Since it’s just 1d it does not need to be heavily optimized and will run fairly quickly anyway.
The Numpy function numpy.roll is particularly useful for performing the advection step.
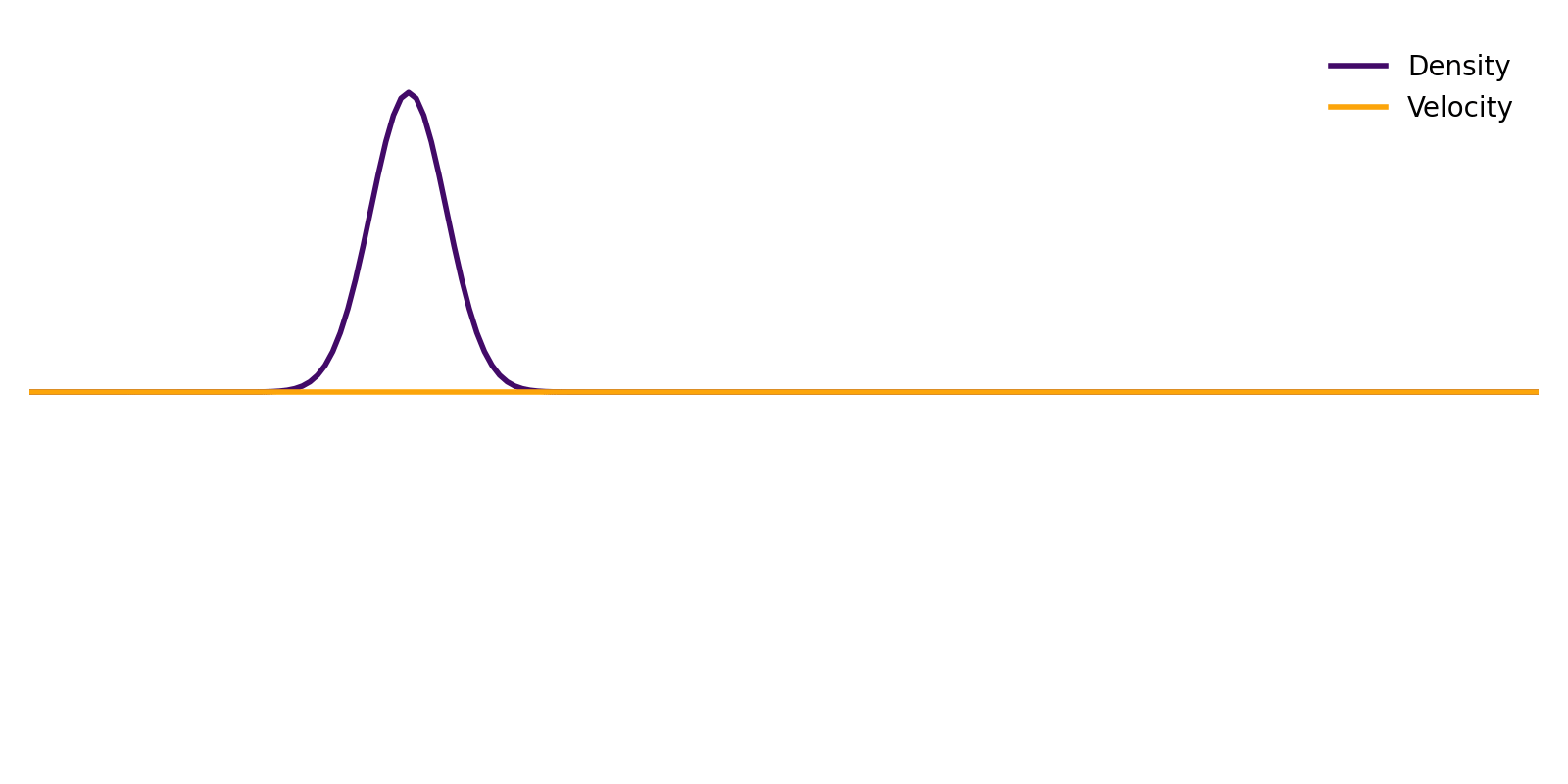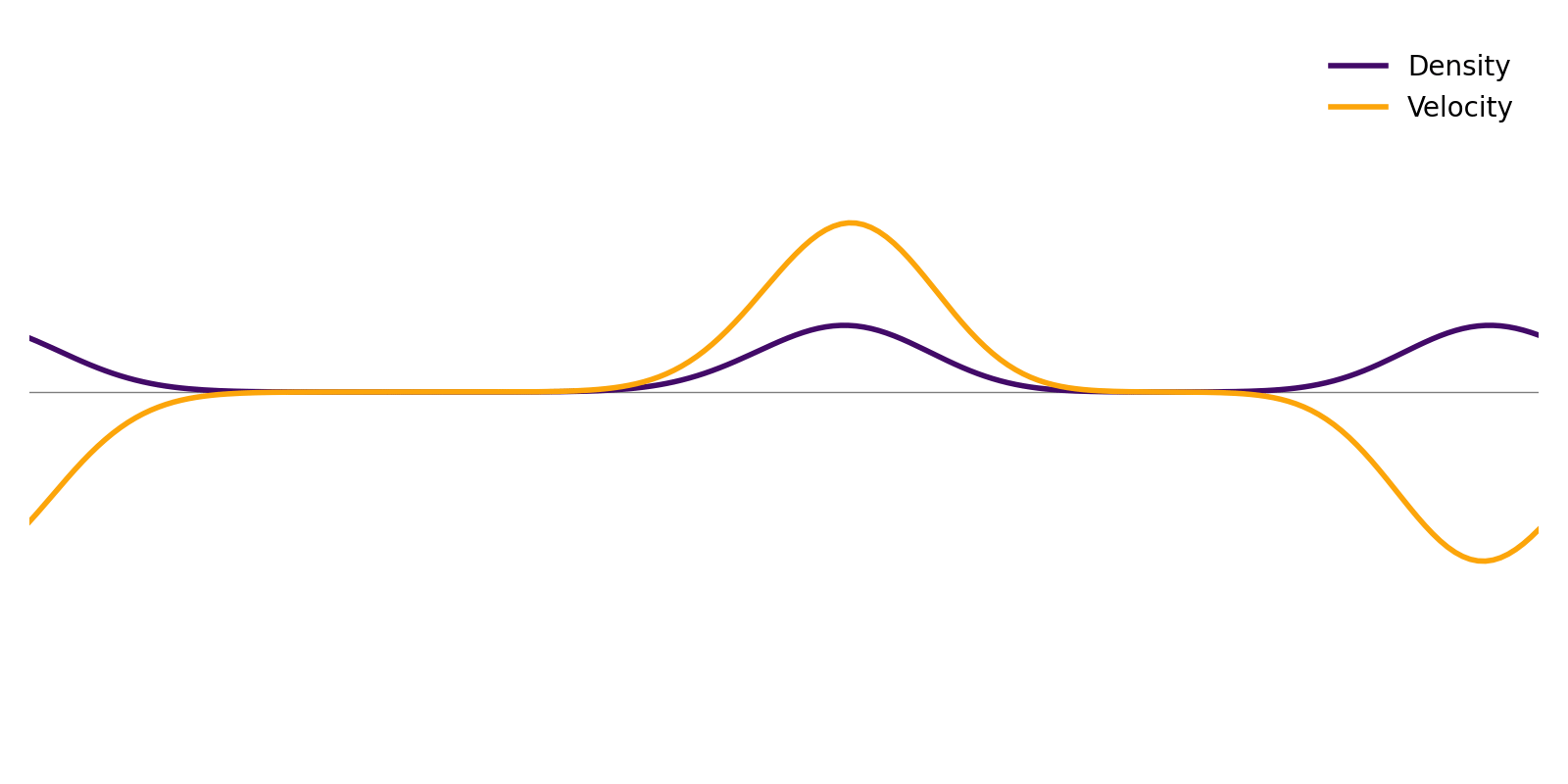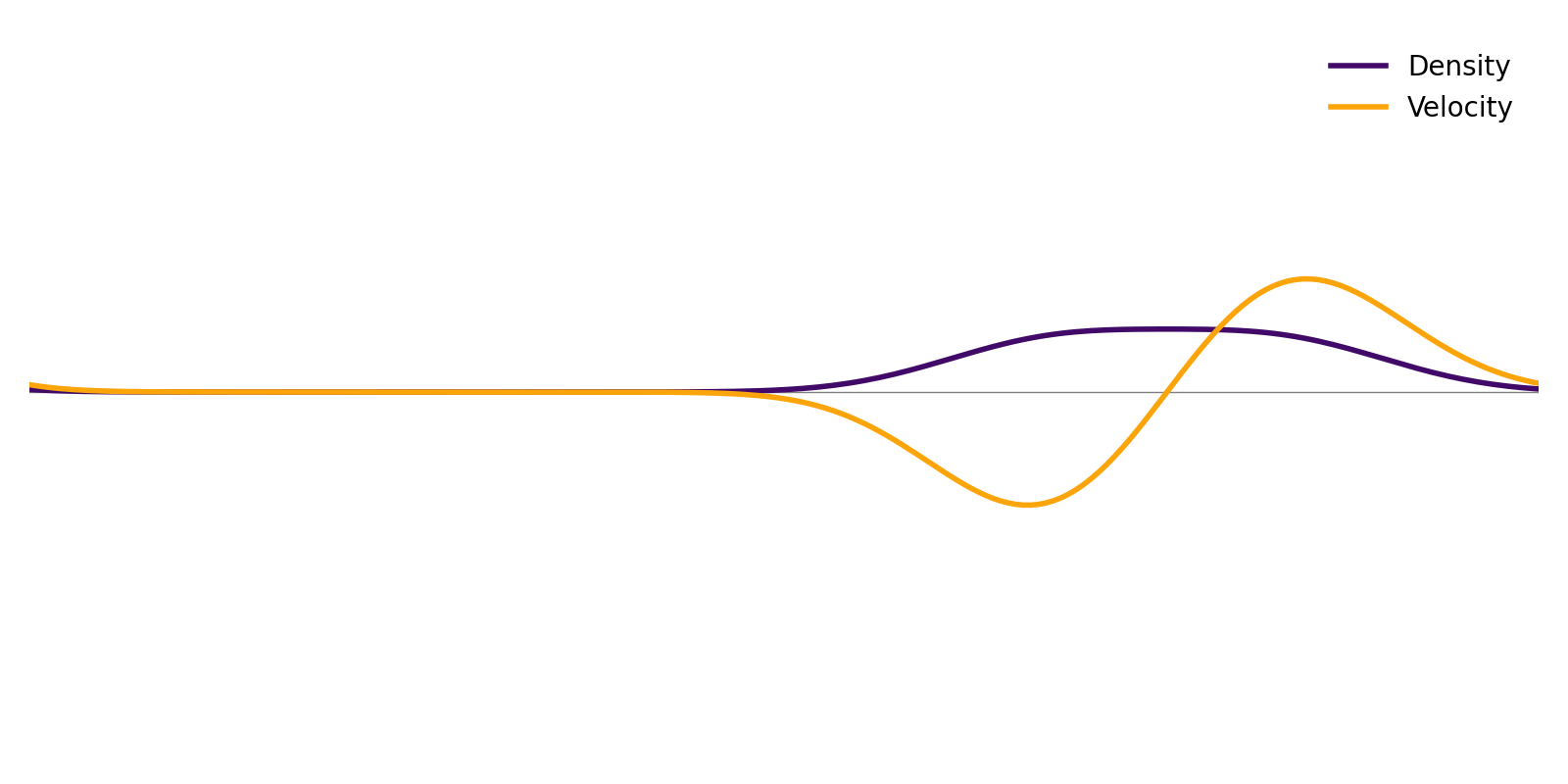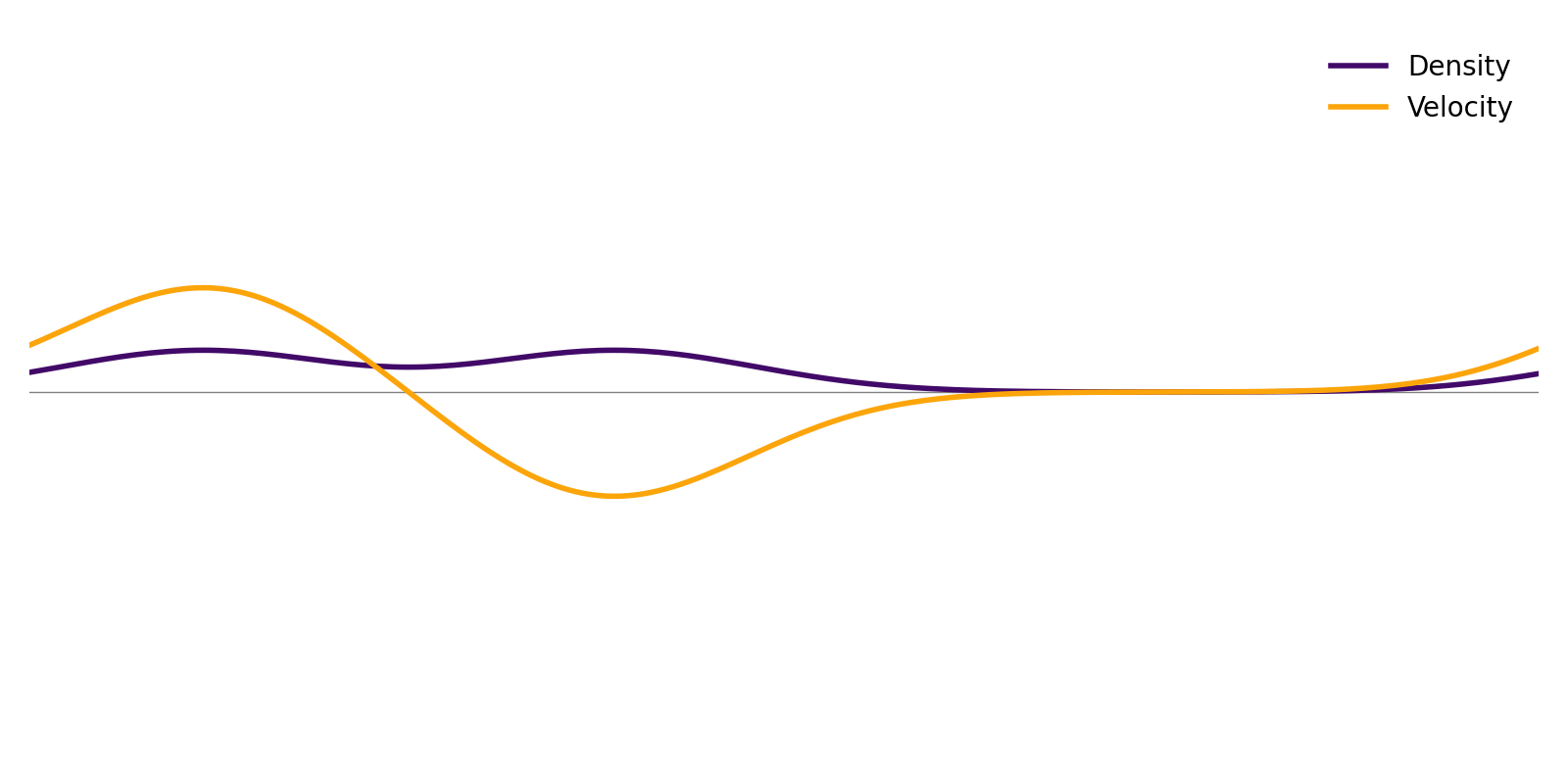
Here is the result of an initially stationary fluid, but with a Gaussian density excess at one location. The fluid is initially at local equilibrium everywhere.